Poincare duality
Tuesday, Mar 31, 2020
Cup products: relative, manifolds with boundary
- * Relative cochains
$C^*(X, A)$ are cochains that vanish on $A$.
- * For manifolds with boundary, there is no co-cycle condition at the boundary, so co-chains are similar to properly embedded submanifolds with boundary.
- * On the other hand, relative co-cycles correspond to closed manifolds.
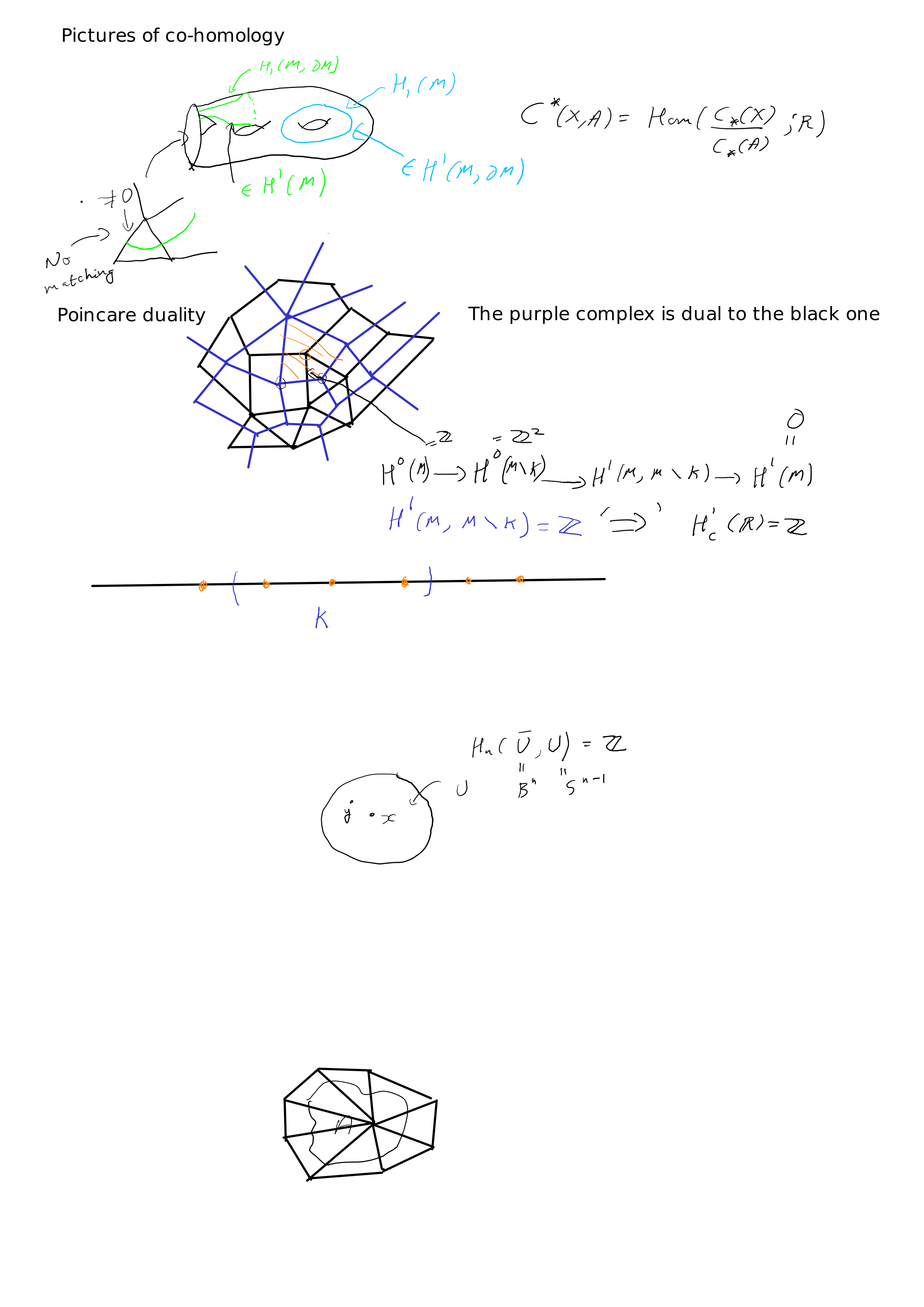
Geometry of Poincaré duality
- * Given a cell decomposition of an oriented $n$-dimensional manifold $M$, we can construct a dual cell decomposition.
- * The cellular chain complex for the dual cell decomposition is the cellular cochain complex of the original cell decomposition.
- * Hence we get
$$H^k(M) = H_{n- k}(M)$$
- * For manifolds with boundary, we have corresponding statements:
$$H^k(M, \partial M) = H_{n- k}(M) \\ H^k(M) = H_{n- k}(M, \partial M) $$
Local homology, restricting homology
- * Fix a space $M$.
- * The local homology at a point is
$H_*(M, M\setminus\{x\})$.
- * By excision,
$H_*(M, M\setminus\{x\}) = H_*(U, U\setminus\{x\})$ if $U$ is open and $x \in U$.
- * In particular if $M$ is a manifold we know the local homology.
- * More generally, for
$A \subset M$ we define $H_*(M\vert A) = H_*(M, M\setminus A). $
- * By excision, if $A$ is closed,
$U\subset M$ is open and $A \subset U$, then $H_*(M\vert A) = H_*(U\vert A)$.
- * This is contravariant in $A$, with restriction; similarly cohomology restricted to $A$ is covariant.
- * WE can similarly define cohomology at $A$, and this is covariant.
Cohomology with compact support
- * Assume $M$ has an exhaustion by compact sets (true for manifolds).
- * Define
$H^*_c(M) = \lim H^*(M, M\setminus K)$ with respect to the ordering of compact sets by inclusions.
- * In the case where $M$ is compact, this is just the ordinary cohomology, but not for $\mathbb{R}$.
Orientations and the Fundamental class
- * Let $M$ be a connected $n$-dimensional manifold.
- * Poincaré duality would imply
$H_n(M; \mathbb{Z}) = H_0(M, \mathbb{Z})= \mathbb{Z}$.
- * For a ring $R$ we define the orientation cover.
- * We consider the rings
$\mathbb{Z}$ and $\mathbb{Z}/2$.
- * A local orientation is a choice of generator
$\mu_x\in H_*(M\vert x)$ for each $x\in M$, which is locally constant, i.e., for $x\in M$ there is an open neighbourhood $U$ of $x$ with closure homeomorphic to a ball such that there exists a generator $\mu_U \in H_n(\bar{U}, \partial U) = \mathbb{Z}$ such that for all $y\in U$, $\mu_y$ is the image of $\mu_U$.
- * We say $M$ is oriented if $M$ has a local orientation at each point.
- * Theorem: If $M$ is closed and $R$-oriented, then
$H_n(M; R)= R$ and $H_k(M, R) = 0$ for $k > n$.
- * We work inductively, so we want a statement for non-compact manifolds.
- * Lemma: Let $M$ be a connected $n$-dimensional manifold and $A\subset M$ be compact.
- * (a)
$H_i(M\vert A; R) = 0$ if $i > n$ and a class $z\in H_n(M\vert A; R)$ is zero if and only if its image is zero in each $H_n(M\vert x; R)$.
- * (b) Given a local orientation
$\mu_x$ there is a class $\mu\in H_n(M\vert A; R)$ that restricts to $\mu_x$ for all $x\in A$.
- * We work inductively, using
$$0 \to H_n(M\vert A\cup B)\to H_N(M\vert A)\oplus H_n(M\vert B)\to H_n(M\vert A\cap B)$$
to conclude that if the result holds for $A$, $B$ and $A \cap B$ then it holds for $A \cup B$.
- * For a class in
$H_n(M\vert A \cup B)$ we chase the diagram.
- * Given a local orientation, find classes
$\mu_A\in H_n(M\vert A)$ and $\mu_B\in H_n(M\vert B)$ satisfying the conclusion, and observe $(\mu_A, \mu_B)$ maps to zero, and use exactness.
- * Using this, we can reduce to the case where
$M = \mathbb{R}^n$.
- * Can deduce for $A$ a linear simplex.
- * Hence deduce for a union of simplices.
- * For a general $A$ in
$\mathbb{R^n}$, we upper bound by a union of simplices so that each simplex intersects $A$.
- * The generator
$\mu\in H_n(M; R)$ we obtain in the compact case is called the fundamental class and denoted $[M]$.
Cap product
- *
$\cap: C_k(X; R) \times C^l(X; R)\to C_{k-l}(X; R)$ is given by
$$\sigma\cap \varphi = \varphi(\sigma\vert_{<v_0, \dots, v_l>})\sigma\vert_{<v_l, \dots, v_k>}$$
- * We have
$\partial (\sigma\cap\varphi) = (-1)^l(\partial \sigma\cap \varphi - \sigma\cap\delta\varphi)$, hence induces pairing on homology and cohomology.
- * In fact, we get
$$H_k(X, A;R)\times H^l(X; R)\to H_{k -l}(X, A; R),\\ H_k(X, A;R)\times H^l(X, A; R)\to H_{k -l}(X; R).$$
- * Further,
$\psi(\sigma\cap \varphi)= (\psi\cup\varphi)(\sigma)$ if $\sigma \in H_k(M)$, $\varphi\in H^l(M)$ and $\psi\in H^{k-l}(M)$.
Poincaré duality
- * The statement of Poincaré duality is in fact that the cap product with the fundamental class is an isomorphism, i.e.,
$D_M : H^k(M) \to H_{n-k}(M)$ given by $\varphi \mapsto [M]\cap \varphi$ is an isomorphism.
- * For (in general) non-compact, $R$-oriented manifold, let
$D_M: H_c^k(M; R)\to H_{n- k}(M; R)$ be the limit of cap products with fundamental class.
- * We see
$$D_M: H_c^k(M; R) \overset{\cong}\to H_{n- k}(M; R).$$
- * This follows inductively.
- * We use maps
$D_M: H^k(M, M\setminus K)\to H_{n-k}(M)$.


